
This is our old website - we are in the process of updating all the information on this site. For current information - check out our main site at
_________________________________________________
Click here for information on our eLearning version of “Introduction to Crowd Science”
_________________________________________________
"Truth is ever to be found in simplicity, and not in the multiplicity and confusion of things. As the world, which to the naked eye exhibits the greatest variety of objects, appears very simple in its internal constitution when surveyed by a philosophical understanding, and so much the simpler by how much the better it is understood." Isaac Newton
Some of the major incidents over the last 30 years.
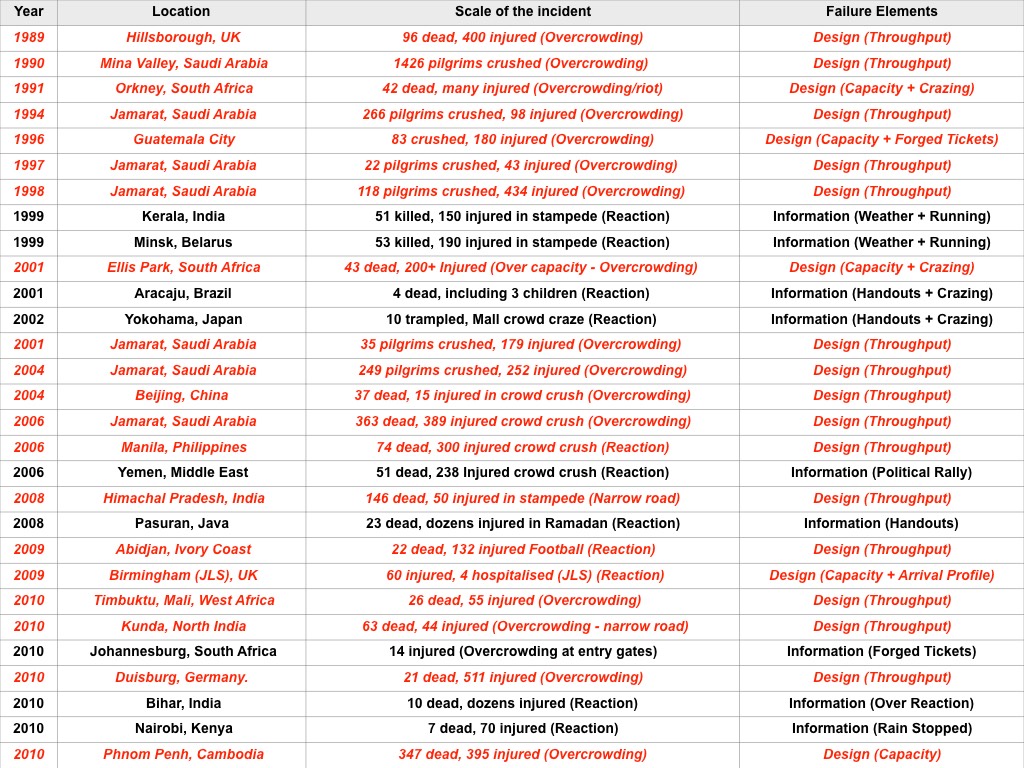
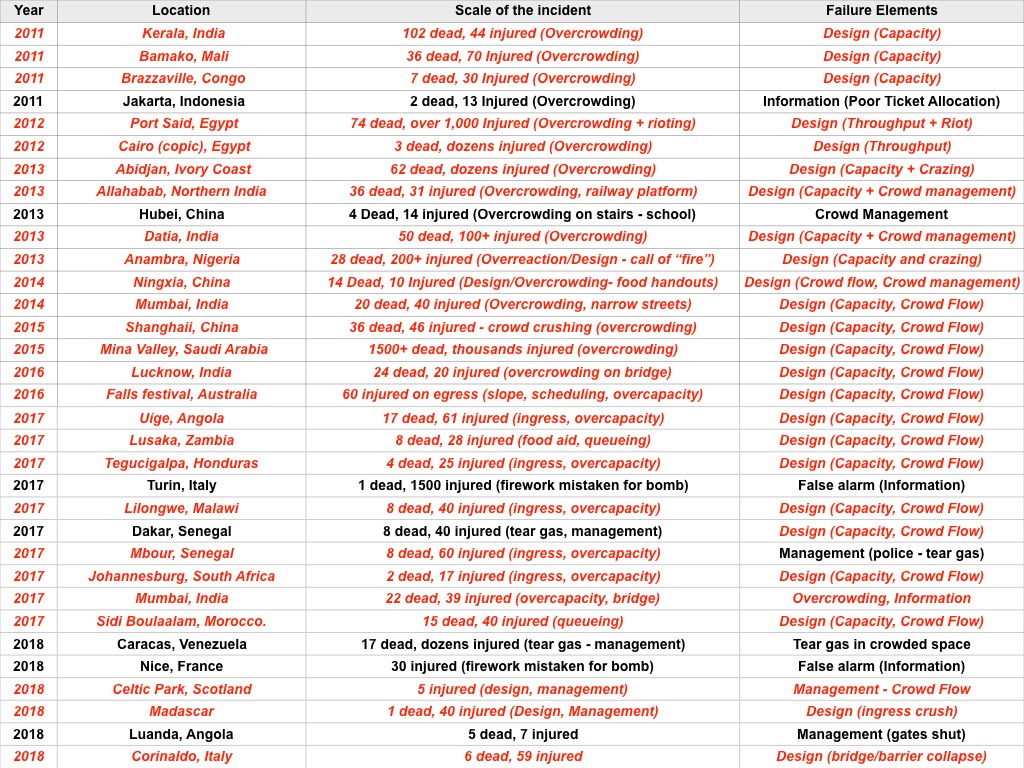
We have highlighted those disasters that have a design issue (shown as red above) as the fundamental (or distal) causality. Namely, the design (space) was not sufficiently robust for the anticipated crowds. Failing to understand the design capacity and throughput, and/or failing to anticipate the crowd numbers is a recipe for disaster, and a fundamental element of crowd risk analysis. This highlights that teaching the principles and applications of how to analyse crowd flow rates, fill times and capacity would have had a significant improvements to crowd safety and saved lives.
My work has focussed on developing educational programs to improving crowd safety through the principles and applications of modelling techniques - not involving computer simulations. Although this was clearly defined in the original thesis, it is still the single most important element to improving crowd safety.
The concept of a model.
Many applications of science make use of models. The term "model" is typically used for a structure which has been built to exhibit features and characteristics of some other object. Generally only some of these features and characteristics will be retained in the model depending upon the use to which it will be put. Sometimes such models are concrete, as is a model aircraft in a wind tunnel experiment, more often models are abstracts or mathematical in nature. There are a number of motives for building a model:
1. The actual exercise of building a model often reveals relationships which were not immediately apparent. As a result a greater understanding is achieved through the modelling process.
2. Having built a model it is usually possible to analyse the model, which helps suggest courses which might not otherwise be apparent.
3. Experimentation is possible with a model whereas it is often not possible (or desirable) to experiment with the object being modelled. It would clearly be dangerous to experiment with large numbers of people moving in and out of a stadium if there was a possibility that anyone may be hurt in the process.
Models, simulations and animations
The development of effective pedestrian simulation systems is important in understanding risk and crowd safety in places of public assembly. However, building a crowd simulation is a complex exercise in applied modelling and it is important that the modeller understands the differences between a simulation, an animation and a model.
What is a model?
Models are mathematical representations of a process and contains the key elements of a system under study. For example activity cycle diagrams, flow charts, algorithms, are all examples of models. Most good models begin with the modeller breaking down a complex process into a series of parts. Mathematical models are often called "toy" systems as they represent a part of a reality.
What is a simulation?
A simulation allows a modeller to test the performance of a system under test. Simulations can take many forms from spreadsheets to three dimensional representations of things moving in space with appropriate physical properties. A simulation can be stochastic or deterministic - it is important that the developer understands the difference between these two types of simulation.
Stochastic models test some probabilistic element (uncertainty) in a system or process. Typical outputs are boundary conditions, upper and lower limits and degree of certainty. If a model is stochastic it needs to output confidence limits so the end user understands that the process under scrutiny has elements of randomness.
A determinist model, as students of chaos theory will know, can also have uncertain outcomes.
Be cautious of simulation outputs that do not state their assumptions. There are many good crowd simulations in the market today, however, these are vastly outweighed by bad, dangerous and misleading crowd simulations.
What is an animation?
An animation (such as a cartoon) can look realistic but have no modelling or simulation properties (such as a series of artistic impressions of how a system may look). Animations can be an output of a model - or just some artists impression of what he/she thinks it may look like. You needs to understand the differences between an animation of a model (or simulation) or a simple animation (to perhaps illustrate some complex process) or an animated simulation. These are all useful tools but animations, simulations and model are three very different types of representations of reality.
Why build a model?
We build models to understand a particular phenomena or characteristic of a system. We build models to understand the relationship between cause and effect. We build models to improve our understanding of a complex environment. We do so because, during the process of building a model, we go through the process of discovery, with discovery comes understanding and with understanding comes control. A complex problem can be analysed and solved by a process of modelling.
Understanding the limits to simulations
In order to understand some aspect of a system it helps to simplify it as much as possible, and to include only those properties and characteristics that are essential to understanding. If you want to determine how an object drops, you don't concern yourself with whether it is new or old, is red of green, has odour or not. You eliminate those things and do not needlessly complicate matters.
Now as you wish to know more and more about any phenomenon, or as the phenomenon becomes more complex, you need more and more elaborate equations, more and more detailed programming, and you end with a computerized simulation that can become harder and harder to grasp.
There is a basic principle involved in the modelling/simulation process called the "least possible simulation" (LPS) which states that a simulation gains in complexity faster than the object being simulated does until, eventually, the simulation catches up with the phenomenon. It was established years ago (Information Theory and the "Shannon Entropy" concept) that you simply cannot produce something that has less information than the thing you are claiming to simulate. Or to put it another way, a system, in it's full complexity, cannot be represented by any simulation smaller than itself.
Thus, no crowd modelling system could claim to model the whole range of human behaviour, without FIRST understanding the WHOLE range of human behaviour. The Shannon principle is simple to express in that, what is "knowable" about a system can be modelled using simulations. There are a lot of models that make false claims (or worse use limiting factors that the modeller is either ignorant of, or chooses to ignore) the user needs to be aware of the limits of his/her system and specifically the Shannon Entropy principle.
One important addition to the Shannon Entropy principle relates to complexity and emergence. Namely that a system of "simple" things can exhibit the apparent complexity of something that has "more information" however this needs further clarification. To quote from my PhD.
From my PhD thesis (Chapter 5)
It is important to define the principles of emergence and how they relate to a simulation. By definition the simulation has to have as few rules as possible to be successful. Those rules also have to represent the characteristics of individuals as they progress through complex geometries, react to differing densities, and act appropriately in a variety of conditions. The conditions can be interpreted by the entities as they navigate the simulation. To prove the concepts and set a goal or objective for the definition of a simulation, we need to outline the principles we wish to demonstrate.
These can be summarised as:
To build an entity level model of the hypothetical mechanisms of a behaviour we must:
- Show that, at a fundamental level, the essential elements actually exist.
- Show, by simulation, that the model is capable of generating the observed behaviour (as an emergent phenomenon).
This leads us to the logical conclusion that if the simulation satisfies the process of the behaviour from the proven underlying mechanisms, we have demonstrated the existence of the phenomenon as a well-constructed scientific object.
Note that this does NOT contradict the principles of Shannon Entropy in that I only claim to model an ELEMENT of crowd behaviour (ie: simulated annealing as a good proxy for evaluating crowd dynamics with respect to risk). I strongly disagree with any system that claims to model "the whole range of human behaviour" to any given situation and would ask for good third party and independent validation before I would entertain any such concept. No one has risen to that challenge yet.
Simulations and animations
Animations are relevant to the process of understanding the dynamics of a complex system. Typically taking the form of computer simulations using graphical representations of a process. They may be real-time animations or replayed animations from a file. It is important to understand the process behind an animation, how it was constructed and what elements it displays.
We can make the following general observations about the simulation approach to decision making. Simulation is most appropriate when the problem is too complex or difficult to solve using another method.
- A model must be developed to represent the various relationships existing in the problem situation.
- A process such as random-number procedures must be employed to generate values for the probabilistic components of the model.
- A bookkeeping procedure must be developed to keep track of what is happening in the simulation process.
- The simulation process must be conducted for many periods in order to establish the long-run averages for the decision alternatives or other changes in the system. Ergodic analysis (long term averages) should be the purpose of the simulation system.
- Local transient effects can skew simulation results - as can bad model building - it is essential that simulation builders be scrutinised in the same way one would scrutinise the simulation system.
- A decision support simulation needs to be validated and open to scrutiny. Good third party validation is essential to be confident of any simulation system.
- Caveat emptor - buyer beware!
How to build a good model
The aims of the model builder should be to construct a model which is easy to understand, easy to detect errors in the process of building a model and easy to compute a solution. To do this one has to spend more time in the analysis of problem and it's requirement than the process of building a model.
You need to break the process into logical, easy to build, easy to test, easy to understand sections. Often it is the process analysis of the problem that leads to a simpler model building process and, as a result, it is easier to understand the results. Links below for more information on:
Crowd risks and the disaster database
Advantages and disadvantages of computer simulation
A complex problem can be analysed and solved using a computer simulation. We can make the following general observations about the simulation approach to decision making.
- Simulation is most appropriate when the problem is too complex or difficult to solve using another method.
- A model must be developed to represent the various relationships existing in the problem situation.
- A process such as random-number procedures must be employed to generate values for the probabilistic components of the model.
- A bookkeeping procedure must be developed to keep track of what is happening in the simulation process.
- Because of the numerous calculations required in most simulations, a computer program or simulator is required.
- The simulation process must be conducted for many days or periods in order to establish the long-run averages for the decision alternatives or other changes in the system.
Simulation should not necessarily be thought of as another technique for finding optimal solutions to problems. However, once a simulation model has been developed, a quantitative analyst may vary certain key design parameters and observe the effect on the output of the computer runs.